Difference between revisions of "Darcy-Weisbach Equation"
| Line 36: | Line 36: | ||
# https://en.wikipedia.org/wiki/Darcy%E2%80%93Weisbach_equation | # https://en.wikipedia.org/wiki/Darcy%E2%80%93Weisbach_equation | ||
# http://www.lessonpaths.com/learn/i/are-you-dense/density-column | # http://www.lessonpaths.com/learn/i/are-you-dense/density-column | ||
| + | |||
| + | [[Category:Siphonic System]] | ||
| + | [[Category:Siphonic System Equations]] | ||
Revision as of 13:04, 14 September 2017
The governing equation used to calculate the expected energy loss due to friction caused by viscous fluid flow through a length of straight pipe or duct.
The inviscid (i.e., frictionless) assumption of Bernoulli is intended to demonstrate a basic principle of energy conversation. However, real fluid flow through a pipe drain or fitting comes at the expense of irreversible energy losses normally referred to as friction. The accepted equation used to calculate the expected energy loss in a fluid system as a result of fluid flow is the Darcy-Weisbach Equation. This equation is expressed as follows:
Darcy-Weisbach Equation
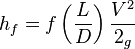
where:
hf = head loss (m) f = friction factor L = length of pipe work (m) d = inner diameter of pipe work (m) V = velocity of fluid (m/s) g = acceleration due to gravity (m/s²)
This equation evaluates energy loss (expressed in feet or fluid).
Known as the pipe-friction equation. Like the coefficient C_f, the friction factor f is dimensionless and is also some function of Reynolds number.
History
Historically this equation arose as a variant on the Prony equation; this variant was developed by Henry Darcy of France, and further refined into the form used today by Julius Weisbach of Saxony in 1845. Initially, data on the variation of fD with velocity was lacking, so the Darcy–Weisbach equation was outperformed at first by the empirical Prony equation in many cases. In later years it was eschewed in many special-case situations in favor of a variety of empirical equations valid only for certain flow regimes, notably the Hazen–Williams equation or the Manning equation, most of which were significantly easier to use in calculations. However, since the advent of the calculator, ease of calculation is no longer a major issue, and so the Darcy–Weisbach equation's generality has made it the preferred one.
Application
In a hydraulic engineering application, it is typical for the volumetric flow Q within a pipe (that is, its productivity) and the head loss per unit length S (the concomitant power consumption) to be the critical important factors. The practical consequence is that, for a fixed volumetric flow rate Q, head loss S decreases with the inverse fifth power of the pipe diameter, D. Doubling the diameter of a pipe of a given schedule (say, ANSI schedule 40) roughly doubles the amount of material required per unit length and thus its installed cost. Meanwhile, the head loss is decreased by a factor 1/32 (about a 97% reduction). Thus the energy consumed in moving a given volumetric flow of the fluid is cut down dramatically for a modest increase in capital cost.
References:
- ASPE Standard 45 Siphonic Roof Drainage
- https://en.wikipedia.org/wiki/Darcy%E2%80%93Weisbach_equation
- http://www.lessonpaths.com/learn/i/are-you-dense/density-column