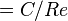Difference between revisions of "Hydraulic Resistance"
(Created page with "[2]There are two types of hydraulic resistance: friction resistance and local resistance. In the former case hydraulic resistance is due to momentum transfer to the solid wall...") |
|||
| Line 1: | Line 1: | ||
[2]There are two types of hydraulic resistance: friction resistance and local resistance. In the former case hydraulic resistance is due to momentum transfer to the solid walls. In the latter case the resistance is caused by dissipation of mechanical energy when the configuration or the direction of flow is sharply changed, by the formation of vortices and secondary flows as a result of the flow breaking away, by the centrifugal forces, etc. To categorize local resistances, we usually refer the resistances of adapters, nozzles, extension pieces, diaphragms, pipeline accessories, swivel knees, pipe entrances, etc. | [2]There are two types of hydraulic resistance: friction resistance and local resistance. In the former case hydraulic resistance is due to momentum transfer to the solid walls. In the latter case the resistance is caused by dissipation of mechanical energy when the configuration or the direction of flow is sharply changed, by the formation of vortices and secondary flows as a result of the flow breaking away, by the centrifugal forces, etc. To categorize local resistances, we usually refer the resistances of adapters, nozzles, extension pieces, diaphragms, pipeline accessories, swivel knees, pipe entrances, etc. | ||
In defining a total resistance (pressure loss Δpf) a conditional superposition is used | In defining a total resistance (pressure loss Δpf) a conditional superposition is used | ||
| − | <math> | + | <math>P_f = P_fr + P_1P^2</math> |
| − | |||
The friction resistance (pressure differential along the channels length) is calculated from Darcy’s empirical formula | The friction resistance (pressure differential along the channels length) is calculated from Darcy’s empirical formula | ||
| − | + | <math>Insert formula here</math> | |
where "f" ̅ is the Moody friction factor (4 times the Fanning friction factor - see Friction Factor), 1 and "D" _"H" = 4S/P are the length and the hydraulic diameter of the channel, ρ is the fluid density, and u is the mean velocity of flow. | where "f" ̅ is the Moody friction factor (4 times the Fanning friction factor - see Friction Factor), 1 and "D" _"H" = 4S/P are the length and the hydraulic diameter of the channel, ρ is the fluid density, and u is the mean velocity of flow. | ||
In order to define the local hydraulic resistance (ΔP1) the Weisbach formula is used | In order to define the local hydraulic resistance (ΔP1) the Weisbach formula is used | ||
| − | + | <math>Insert formula here</math> | |
Where , is the coefficient of local resistance. | Where , is the coefficient of local resistance. | ||
For flow in smooth channels the friction factor f depends on the flow conditions and is only a function of Re = ūDH/ν. For a laminar flow, the value for straight pipes is determined from the Poiseuille formula: | For flow in smooth channels the friction factor f depends on the flow conditions and is only a function of Re = ūDH/ν. For a laminar flow, the value for straight pipes is determined from the Poiseuille formula: | ||
| − | + | <math> = C/Re</math> | |
== References == | == References == | ||
#http://www.thermopedia.com/content/857/ | #http://www.thermopedia.com/content/857/ | ||
Latest revision as of 17:02, 12 September 2017
[2]There are two types of hydraulic resistance: friction resistance and local resistance. In the former case hydraulic resistance is due to momentum transfer to the solid walls. In the latter case the resistance is caused by dissipation of mechanical energy when the configuration or the direction of flow is sharply changed, by the formation of vortices and secondary flows as a result of the flow breaking away, by the centrifugal forces, etc. To categorize local resistances, we usually refer the resistances of adapters, nozzles, extension pieces, diaphragms, pipeline accessories, swivel knees, pipe entrances, etc.
In defining a total resistance (pressure loss Δpf) a conditional superposition is used
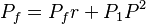
The friction resistance (pressure differential along the channels length) is calculated from Darcy’s empirical formula
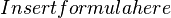where "f" ̅ is the Moody friction factor (4 times the Fanning friction factor - see Friction Factor), 1 and "D" _"H" = 4S/P are the length and the hydraulic diameter of the channel, ρ is the fluid density, and u is the mean velocity of flow.
In order to define the local hydraulic resistance (ΔP1) the Weisbach formula is used
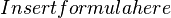Where , is the coefficient of local resistance.
For flow in smooth channels the friction factor f depends on the flow conditions and is only a function of Re = ūDH/ν. For a laminar flow, the value for straight pipes is determined from the Poiseuille formula:
