Poisson's ratio
Poisson ratio is one of the important criteria to be considered in pipe selection where the system may be subjected to sub-atmospheric pressure (e.g. Siphonic drainage systems). In general, a lower value in Poisson ratio provides better strength against collapse of pipe due to sub-atmospheric pressure.
In evaluating the limiting or maximum pressures, forces and deflections on plastic pipe, fittings and components covered by this standard, the material properties listed below are assumed at an operating temperature of 20°C (68°F).[1]
| Material Properties at an Operating Temperature of 20°C (68°F) | |||||
|---|---|---|---|---|---|
| Property/ Material | Tensile Modulus of Elasticity | Creep Modulus | Poisson’s Ratio | Rate of Thermal Expansion | |
| Symbol | 
|

|
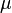
|
| |
| Units | Mpa(psi) | Mpa(psi) | dimensionless | cm/cm/°C (ft/ft/°F) | |
| ABS | 2,206 (320,000) | Varies (refer to 8.2.2) | 0.35 | 10.3 E-5 (5.7 E-5) | |
| HPDE | 862 (125,000) | 0.45 | 18.0 E-5 (10.0 E-5) | ||
| PVC | 2,827 (410,000) | 0.35 | 5.2 E-5 (3.0 E-5) | ||
| Test Method | ASTM D638 | ISO 899 | ASTM E132 | ASTM D696 | |
Calculation of allowable pressure 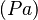 : The minimum required pipe wall thickness
: The minimum required pipe wall thickness 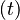 shall be based on Equations 8.1 and 8.2 in Table 8.2 and the mechanical and dimensional properties of the pipe material evaluated. Equations 8.1 and 8.2 apply for a long cyclindrical tube of length L and wall thickness t under uniform external pressure with
shall be based on Equations 8.1 and 8.2 in Table 8.2 and the mechanical and dimensional properties of the pipe material evaluated. Equations 8.1 and 8.2 apply for a long cyclindrical tube of length L and wall thickness t under uniform external pressure with 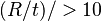 .
.
| Table 8.2 Pipe Wall Thickness Calculations | |||||
|---|---|---|---|---|---|
| Equation 8.1 When, |
Equation 8.2 When | ||||
![P_{cr}= \frac{E_c}{3(1-\mu^2)} \Bigg[ \frac{t}{R} \Bigg]^3](/images/math/a/9/e/a9eae55e231d6bffd5e002ca1ce78246.png)
|
![P_{cr}= 0.807 \Bigg[ \frac{E_c t^2}{LR} \Bigg] \Bigg[ \Big( \frac{1}{1-\mu^2} \Big) \Big( \frac{t}{R} \Big)^2 \Bigg] ^{0.25}](/images/math/8/5/5/8559cae769ac49b70a6cc937970a6a3e.png)
| ||||
When, 
|
When, 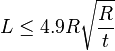
| ||||
The parameter  is the elastic creep modulus at the specified time of loading. The allowable pressure
is the elastic creep modulus at the specified time of loading. The allowable pressure 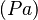 shall be the calculated critical buckling pressure divided by the factor of safety (FS) as in equation below:
shall be the calculated critical buckling pressure divided by the factor of safety (FS) as in equation below:
Equation 8.3:
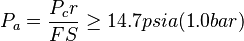
- Poisson's ratio is the ratio of the relative contraction strain (or transverse strain) normal to the applied load - to the relative extension strain (or axial strain) in the direction of the applied load [2]
Poisson's Ratio can be expressed as;
μ = - εt / εl where μ = Poisson's ratio εt = transverse strain εl = longitudinal or axial strain
Strain can be expressed as;
ε = dl / L where dl = change in length (m, ft) L = initial length (m, ft) For most common materials the Poisson's ratio is in the range 0 - 0.5. μ = Poisson’s Ratio (dimensionless)
- Poisson's ratio describes the relative change of the lateral dimension of an object when the load is applied on the longitudinal direction and vice versa. (See reference video link [1])
References
- ↑ ASPE Standard 45
- ↑ http://www.engineeringtoolbox.com/poissons-ratio-d_1224.html