Colebrook-White Equation
Revision as of 17:02, 8 September 2017 by Joceil.infante (talk | contribs)
[1] The governing equation used to calculate the expected friction loss factor (f) used in the Darcy-Weisbach Equation. The equation is a function of pipe surface roughness, pipe diameter, fluid viscosity and fluid velocity.
[2] The loss of energy head, 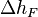 , due to wall friction in a length of pipe between points 1 and 2 in a system is given by:
, due to wall friction in a length of pipe between points 1 and 2 in a system is given by:
The frictional head loss gradient, 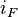 , can be determined from the Colebrook-White equation, which for pipes flowing 100% full of water may be written in the form;
, can be determined from the Colebrook-White equation, which for pipes flowing 100% full of water may be written in the form;
NOTE: An iterative method of solution is required to find the head loss gradient,, from equation because this quantity also appears on the right-hand side of the equation.
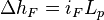
![i_F = ( \frac{u^2}{8gd_1} ) { \Big\{ {log_{10}} [ \frac{k_p}{371d_1} + \frac{1.775v} {\sqrt{gi_F d_i}^3} ]}^{-2}](/images/math/f/4/c/f4c5e0254673e1b7c0f96348dd30da87.png)