Bernoulli's Equation

(See also Bernoulli's principle)

• Common name for the fluid energy equation. An energy balance equation demonstrating the conservation of three major states - static pressure energy, kinetic energy (velocity pressure) and potential energy. Also referred to as Bernoulli’s Principle.

Daniel Bernoulli presented the Bernoulli’s theorem in 1738;

• Bernoulli’s equation is one of the fundamental equations of fluid mechanics and is the primary equation upon which is siphonic drainage design is based.

The equation is an energy balance relationship stating that a fluid in either rest or in motion possesses three fundamental forms of energy. A fluid has a static pressure energy that represents the work performed to compress the fluid system. It also has a kinetic energy that represents the work performed on the fluid system to bring the fluid from rest to a certain velocity. Finally, the fluid also possesses a potential energy as a result of its elevation in a gravity field. The sum of these energy states, according to Bernoulli, is conserved even though the system energy states may be transferred from one form to another. The form of Bernoulli’s Equation used here makes three main assumptions;

1. The fluid is incompressible and inviscid.
2. No work is done on the system or performed by the system.
3. The system is adiabatic.

Bernoulli’s Equation is expressed as follows;

$\frac{P_1}{\rho g}+\frac{V_1^2}{2g}+Z_1=\frac{P_2}{\rho g}+\frac{V_2^2}{2g}+Z_2$

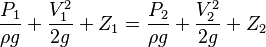
(The subscripts 1 and 2 represent two locations along a streamline or two process end states within the fluid system.)

• The Energy Equation for steady flow of incompressible fluids

$\frac{P_1}{y}+Z_1+\frac{V_1^2}{2g}=\frac{P_2}{y}+Z_2+\frac{V_2^2}{2g}$

and from this it follows that

$\frac{P_1}{y}+Z+\frac{V^2}{2g}=constant$

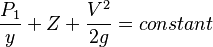
Note that Bernoulli’s theorem is for a frictionless incompressible fluid. However, it can be applied to real incompressible fluids with good results in situations where frictional effects are very small.

• When a fluid flows into a narrower channel, its speed increases. That means its kinetic energy also increases. Where does that change in kinetic energy come from? The increased kinetic energy comes from the net work done on the fluid to push it into the channel and the work done on the fluid by the gravitational force, if the fluid changes vertical position. Recall the work-energy theorem,

$W_{net}=\frac{1}{2}mv^2-\frac{1}{2}mv_{0^2}$

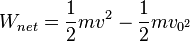
There is a pressure difference when the channel narrows. This pressure difference results in a net force on the fluid: recall that pressure times area equals force. The net work done increases the fluid’s kinetic energy. As a result, the pressure will drop in a rapidly-moving fluid, whether or not the fluid is confined to a tube.

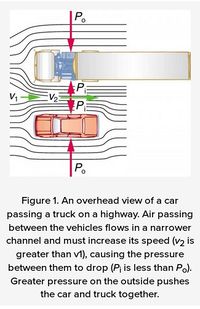
There are a number of common examples of pressure dropping in rapidly-moving fluids. Shower curtains have a disagreeable habit of bulging into the shower stall when the shower is on. The high-velocity stream of water and air creates a region of lower pressure inside the shower, and standard atmospheric pressure on the other side. The pressure difference results in a net force inward pushing the curtain in. You may also have noticed that when passing a truck on the highway, your car tends to veer toward it. The reason is the same—the high velocity of the air between the car and the truck creates a region of lower pressure, and the vehicles are pushed together by greater pressure on the outside. (See Figure 1.) This effect was observed as far back as the mid-1800s, when it was found that trains passing in opposite directions tipped precariously toward one another. The relationship between pressure and velocity in fluids is described quantitatively by Bernoulli’s equation, named after its discoverer, the Swiss scientist Daniel Bernoulli (1700–1782). Bernoulli’s equation states that for an incompressible, frictionless fluid, the following sum is constant:

$P+\frac{1}{2}pv^2+pgh=constant$

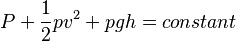
where P is the absolute pressure, ρ is the fluid density, v is the velocity of the fluid, h is the height above some reference point, and g is the acceleration due to gravity. If we follow a small volume of fluid along its path, various quantities in the sum may change, but the total remains constant. Let the subscripts 1 and 2 refer to any two points along the path that the bit of fluid follows; Bernoulli’s equation becomes;

$P_1+\frac{1}{2}\rho v_1^2+\rho gh_1=P_2+\frac{1}{2}\rho v_2^2+ \rho pgh_2$

Bernoulli’s equation is a form of the conservation of energy principle. Note that the second and third terms are the kinetic and potential energy with m replaced by ρ. In fact, each term in the equation has units of energy per unit volume. We can prove this for the second term by substituting $\rho=\frac{m}{V}$ into it and gathering terms: $\frac{1}{2}\rho v^2=\frac{\frac{1}{2}mv^2}{V}=\frac{KE}{V}$

So $\frac{1}{2}\rho v^2$

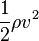
is the kinetic energy per unit volume. Making the same substitution into the third term in the equation, we find

$\rho gh=\frac{mgh}{V}=\frac{PE_g}{V}$

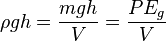
So ρgh is the gravitational potential energy per unit volume. Note that pressure P has units of energy per unit volume, too. Since 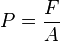$P = \frac{F}{A}$ , its units are 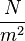$\frac{N}{m^2}$. If we multiply these by 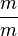$\frac{m}{m}$, we obtain 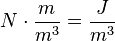$N \cdot \frac{m}{m^3} = \frac{J}{m^3}$ , or energy per unit volume. Bernoulli’s equation is, in fact, just a convenient statement of conservation of energy for an incompressible fluid in the absence of friction.

Application of Bernoulli’s Equation

Bernoulli's equation states that for an incompressible and inviscid fluid, the total mechanical energy of the fluid is constant. (An inviscid fluid is assumed to be an ideal fluid with no viscosity.)

The total mechanical energy of a fluid exists in two forms: potential and kinetic. The kinetic energy of the fluid is stored in static pressure, 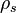$\rho_s$ , and dynamic pressure, 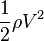$\frac{1}{2} \rho V^2$, where \rho is the fluid density in (SI unit 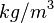$kg/m^3$) and V is the fluid velocity (SI unit: $m/s$). The SI unit of static pressure and dynamic pressure is the pascal. Static pressure is simply the pressure at a given point in the fluid; dynamic pressure is the kinetic energy per unit volume of a fluid particle. Thus, a fluid will not have dynamic pressure unless it is moving. Therefore, if there is no change in potential energy along a streamline, Bernoulli's equation implies that the total energy along that streamline is constant and is a balance between static and dynamic pressure. Mathematically, the previous statement implies: $p+\frac{1}{2}V^2=constant$

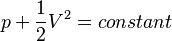
along a streamline. If changes there are significant changes in height or if the fluid density is high, the change in potential energy should not be ignored and can be accounted for with, $\vartriangle PE + \rho g \vartriangle h$

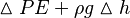
This simply adds another term to the above version of the Bernoulli equation and results in $\rho_s+\frac{1}{2}\rho V^2+\rho g\vartriangle h = constant$

References

1. ASPE Standard 45 Siphonic Roof Drainage
2. Fluid Mechanics with Engineering Applications p.93
3. https://courses.lumenlearning.com/physics/chapter/12-2-bernoullis-equation/
4. https://www.boundless.com/physics/textbooks/boundless-physics-textbook/fluid-dynamics-and-its-applications-11/bernoulli-s-equation-99/application-of-bernoulli-s-equation-pressure-and-speed-357-4588/
5. http://philschatz.com/physics-book/contents/m42206.html